25.09.2019
Solving inequalities with a parameter by a graphical method. §2. Quadratic equations and inequalities with a parameter
Solving inequalities with a parameter.
Inequalities that have the form ax > b, ax< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются linear inequalities.
The principles for solving linear inequalities with a parameter are very similar to the principles for solving linear equations with a parameter.
Example 1
Solve the inequality 5x - a > ax + 3.
Solution.
First, let's transform the original inequality:
5x - ax > a + 3, we take out the brackets x on the left side of the inequality:
(5 - a) x > a + 3. Now consider the possible cases for the parameter a:
If a > 5 then x< (а + 3) / (5 – а).
If a = 5, then there are no solutions.
If a< 5, то x >(a + 3) / (5 - a).
This solution will be the answer to the inequality.
Example 2
Solve the inequality x(a - 2) / (a - 1) - 2a / 3 ≤ 2x - a for a ≠ 1.
Solution.
Let's transform the original inequality:
x(a - 2) / (a - 1) - 2x ≤ 2a/3 - a;
Ah/(a – 1) ≤ -a/3. Multiply by (-1) both parts of the inequality, we get:
ax/(a – 1) ≥ a/3. Let's explore the possible cases for the parameter a:
1 case. Let a/(a – 1) > 0 or a € (-∞; 0)ᴗ(1; +∞). Then x ≥ (а – 1)/3.
2nd case. Let a/(а – 1) = 0, i.e. a = 0. Then x is any real number.
3rd case. Let a/(а – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.
Answer: x € [(a - 1) / 3; +∞) for a € (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] for a € (0; 1);
x € R for a = 0.
Example 3
Solve the inequality |1 + x| ≤ ax with respect to x.
Solution.
It follows from the condition that the right side of the inequality ax must be non-negative, i.e. ax ≥ 0. By the modulo expansion rule, the inequality |1 + x| ≤ ax we have a double inequality
Ax ≤ 1 + x ≤ ax. We rewrite the result in the form of a system:
(ax ≥ 1 + x;
(-ax ≤ 1 + x.
Let's transform to the form:
((а – 1)x ≥ 1;
((a + 1)x ≥ -1.
We investigate the resulting system on intervals and at points (Fig. 1):
For a ≤ -1 x € (-∞; 1/(a - 1)].
At -1< а < 0 x € [-1/(а – 1); 1/(а – 1)].
When a \u003d 0 x \u003d -1.
At 0< а ≤ 1 решений нет.
Graphical method for solving inequalities
Plotting greatly simplifies the solution of equations containing a parameter. The use of the graphical method in solving inequalities with a parameter is even clearer and more expedient.
Graphical solution of inequalities of the form f(x) ≥ g(x) means finding the values of the variable x for which the graph of the function f(x) lies above the graph of the function g(x). To do this, it is always necessary to find the intersection points of the graphs (if they exist).
Example 1
Solve the inequality |x + 5|< bx.
Solution.
We build graphs of functions y = |x + 5| and y = bx (Fig. 2). The solution of the inequality will be those values of the variable x for which the graph of the function y = |x + 5| will be below the graph of the function y = bx. 
The figure shows:
1) For b > 1, the lines intersect. The abscissa of the intersection point of the graphs of these functions is the solution of the equation x + 5 = bx, whence x = 5/(b - 1). The graph y \u003d bx is higher for x from the interval (5 / (b - 1); +∞), which means that this set is the solution to the inequality.
2) Similarly, we find that at -1< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).
3) For b ≤ -1 x € (-∞; 5/(b - 1)).
4) For 0 ≤ b ≤ 1, the graphs do not intersect, which means that the inequality has no solutions.
Answer: x € (-∞; 5/(b - 1)) for b ≤ -1;
x € (-5/(b + 1); 5/(b – 1)) at -1< b < 0;
there are no solutions for 0 ≤ b ≤ 1; x € (5/(b – 1); +∞) for b > 1.
Example 2
Solve the inequality a(a + 1)x > (a + 1)(a + 4).
Solution.
1) Let's find the "control" values for the parameter a: a 1 = 0, a 2 = -1.
2) Let's solve this inequality on each subset of real numbers: (-∞; -1); (-1); (-10); (0); (0; +∞).
a) a< -1, из данного неравенства следует, что х >(a + 4)/a;
b) a \u003d -1, then this inequality will take the form 0 x > 0 - there are no solutions;
c)-1< a < 0, из данного неравенства следует, что х < (a + 4)/a;
d) a = 0, then this inequality has the form 0 x > 4 – there are no solutions;
e) a > 0, this inequality implies that x > (a + 4)/a.
Example 3
Solve the inequality |2 – |x||< a – x.
Solution.
We plot the function y = |2 – |x|| (Fig. 3) and consider all possible cases of the location of the line y \u003d -x + a. 
Answer: the inequality has no solutions for a ≤ -2;
x € (-∞; (a - 2)/2) with a € (-2; 2];
x € (-∞; (a + 2)/2) for a > 2.
When solving various problems, equations and inequalities with parameters, a significant number of heuristic techniques open up, which can then be successfully applied in any other branches of mathematics.
Tasks with parameters play important role in the formation of logical thinking and mathematical culture. That is why, having mastered the methods of solving problems with parameters, you will successfully cope with other problems.
Do you have any questions? Don't know how to solve inequalities?
To get the help of a tutor - register.
The first lesson is free!
site, with full or partial copying of the material, a link to the source is required.
Preview:
MINISTRY OF EDUCATION OF THE MOSCOW REGION
GOU NPO Vocational School No. 37
PROJECT:
OF QUADRATIVE EQUATIONS AND INEQUALITIES WITH PARAMETERS»
Performed -
Matsuk Galina Nikolaevna,
Mathematics teacher, NPO
vocational school No. 37 MO.
G.Noginsk, 2011
1. Introduction
4. Technique for solving quadratic equations under initial conditions.
6. Technique for solving quadratic inequalities with parameters in general form.
7. Method for solving quadratic inequalities under initial conditions.
8. Conclusion.
9. Literature.
- Introduction.
The main task of teaching mathematics in vocational school is to ensure a strong and conscious mastery of the system of mathematical knowledge and skills necessary for students Everyday life And labor activity sufficient to study related disciplines and continue education, as well as in professional activity requiring a sufficiently high mathematical culture.
Profiled teaching of mathematics is carried out through the solution of applied problems related to professions in metalworking, electrical work, and woodworking. For life in modern society important is the formation of a mathematical style of communication, manifested in certain mental skills. Tasks with parameters have diagnostic and prognostic value. With their help, you can check the knowledge of the main sections of elementary mathematics, the level of logical thinking, the initial skills of research work.
Teaching tasks with parameters requires great mental and volitional efforts from students, developed attention, and the development of such qualities as activity, creative initiative, and collective cognitive work. Tasks with parameters are oriented for studying during a generalizing repetition in the 2nd year in preparation for the final state certification and in the 3rd year in additional classes in the preparation of students who have expressed a desire to take the final exams in the form of the Unified State Examination.
The main direction of modernization of mathematical education is the development of mechanisms for final certification through the introduction of the Unified State Examination. In math assignments last years tasks with parameters are introduced. Such tasks are mandatory for entrance exams to universities. The appearance of such tasks is very important, since they are used to check the technique of mastering the formulas of elementary mathematics, methods for solving equations and inequalities, the ability to build a logical chain of reasoning, the level of logical thinking of the applicant. Analysis of previous USE results over the past few years shows that graduates solve such tasks with great difficulty, and many do not even start them. Most either do not cope with such tasks at all, or give cumbersome calculations. The reason for this is the lack of a system of tasks on this topic in school textbooks. In this regard, it became necessary to conduct special topics in graduate groups in preparation for exams on solving problems with parameters and applied problems related to professional orientation.
The study of these topics is intended for 3rd year students who want to learn how to solve problems advanced level difficulties in algebra and the beginnings of analysis. The solution of such problems causes considerable difficulties for them. This is due to the fact that each equation or inequality with parameters is a whole class of ordinary equations and inequalities, for each of which a solution must be obtained.
In the process of solving problems with parameters, the arsenal of techniques and methods of human thinking naturally includes induction and deduction, generalization and concretization, analysis, classification and systematization, and analogy. Since the curriculum in vocational schools provides for consultations in mathematics, which are available in the schedule of training sessions, it is advisable for students who have sufficient mathematical training, who are interested in the subject being studied, with the further goal of entering a university, to use these hours to solve problems with parameters for preparing for olympiads, mathematical competitions, various kinds of exams, in particular the USE. Especially important is the solution of such problems for applied and practical nature, which will help in carrying out various studies.
2. Goals, main tasks, methods, technologies, knowledge requirements.
Project goals:
- Formation of skills and abilities in solving problems with parameters, reduced to the study of quadratic equations and inequalities.
- Formation of interest in the subject, development of mathematical abilities, preparation for the exam.
- Expansion of mathematical ideas about techniques and methods for solving equations and inequalities.
- Development of logical thinking and research skills.
- Introduction to creative, research and cognitive activities.
- Providing conditions for independent creative work.
- Education in students of mental and volitional efforts, developed attention, activity, creative initiative, skills of collective cognitive work.
The main tasks of the project:
- Provide students with the opportunity to realize their interest in mathematics and individual opportunities for its development.
- Contribute to the assimilation of factual knowledge and skills.
- Show the practical significance of tasks with parameters in the field of applied research.
- To teach how to solve standard and non-standard equations and inequalities.
- To deepen knowledge in mathematics, providing for the formation of a sustainable interest in the subject.
- To identify and develop the mathematical abilities of students.
- Provide preparation for admission to universities.
- Provide training for professional activities that require a high mathematical culture.
- Organize research and project activities, contributing to the development of intellectual and communicative qualities.
Methods used in conducting classes:
- Lecture - for the transfer of theoretical material, accompanied by a conversation with students.
- Seminars - to consolidate the material on the discussion of the theory.
- Workshops - for solving mathematical problems.
- Discussions - to argue options for their decisions.
- Various forms of group and individual activity.
- Research activity, which is organized through: work with didactic material, preparation of messages, defense of abstracts and creative works.
- Lectures are presentations using a computer and a projector.
Used technologies:
- Lecture and seminar system of education.
- Information and communication technologies.
- A research method in teaching aimed at developing mental abilities.
- Problem-based learning, providing motivation for research by posing a problem, discussion various options Problems.
- The technology of the activity method, which helps to bring out the cognitive interests of students.
Requirements for the knowledge of students.
As a result of studying various ways to solve quadratic equations and inequalities with parameters, students should acquire the skills to:
- To firmly master the concept of a parameter in a quadratic equation and a quadratic inequality;
- Be able to solve quadratic equations with parameters.
- Be able to solve quadratic inequalities with parameters.
- Find the roots of a quadratic function.
- Build graphs of quadratic functions.
- Explore a quadratic trinomial.
- Apply rational methods of identical transformations.
- Use the most commonly used heuristics.
- Be able to apply the acquired knowledge when working on a personal computer.
Forms of control.
- Lessons - self-assessment and assessment of comrades.
- Presentation of educational projects.
- Testing.
- Rating - table.
- Homework assignments from collections of exams from previous years.
- Test papers.
3. Technique for solving quadratic equations with parameters in general form.
Do not be afraid of tasks with parameters. First of all, when solving equations and inequalities with parameters, you need to do what is done when solving any equation and inequality - bring the given equations or inequalities to more plain sight, if possible: factorize a rational expression, reduce, take the factor out of brackets, etc. There are tasks that can be divided into two large classes.
The first class includes examples in which it is necessary to solve an equation or an inequality for all possible values of the parameter.
The second class includes examples in which it is necessary to find not all possible solutions, but only those that satisfy some additional conditions. The class of such problems is inexhaustible.
The most understandable way for students to solve such problems is that they first find all solutions, and then select those that satisfy additional conditions.
When solving problems with parameters, it is sometimes convenient to build graphs in the usual plane (x, y), and sometimes it is better to consider graphs in the (x, a) plane, where x is an independent variable, and “a” is a parameter. This is primarily possible in a problem where you have to build familiar elementary graphs: straight lines, parabolas, circles, etc. In addition, sketches of graphs sometimes help to visually see the “progress” of the solution.
When solving the equations f (x, a) = 0 and the inequalities f (x, a) > 0, it must be remembered that, first of all, the solution is considered for those values of the parameter for which the coefficient at the highest degree x of the square trinomial f (x ,a), thereby lowering the degree. Quadratic equation A(a) x 2 + B(a) x + C(a) = 0 at A(a) = 0 becomes linear if B(a) ≠ 0, and the methods for solving quadratic and linear equations are different.
Let's recall the basic formulas for working with quadratic equations.
Equation of the form ax 2 + in + c \u003d 0, where x R are unknowns, a, c, c are expressions that depend only on parameters, and a ≠ 0 is called a quadratic equation, and D = b 2 - 4ac is called the discriminant of a square trinomial.
If D
If D > 0, then the equation has two different roots
x 1 \u003d, x 2 \u003d, and then ah 2 + in + c \u003d a (x - x 1) (x - x 2).
These roots are connected through the coefficients of the equation by the Vieta formulas
If D = 0, then the equation has two coinciding roots x 1 \u003d x 2 \u003d, and then ax 2 + in + c \u003d a (x - x 1) 2 . In this case, the equation is said to have one solution.
When , i.e. \u003d 2k, the roots of the quadratic equation are determined by the formula x 1,2 = ,
To solve the given quadratic equation x 2 + px + q = 0
The formula x is used 1,2 = - , as well as the Vieta formulas
Examples. Solve Equations:
Example 1. +=
Solution:
When a ≠ - 1, x ≠ 2 we get x 2 + 2ax - 3c + 4 = 0 and roots
x 1 \u003d - a -, x 2 \u003d -a + , existing at
А 2 + 2а – 4 0, i.e. at
Now let's check if there are any such a for which either x 1 or x 2 is 2. Substitute in the quadratic equation x \u003d 2, while we get a \u003d - 8.
The second root in this case is(according to the Vieta theorem) and for a = - 8 it is equal to 14.
Answer: for a = - 8 the only solution is x = 14;
If a (- ∞; - 8) (- 8; - 4) (1; + ∞) – two roots x 1 and x 2;
If a = - the only solution x =respectively;
If a (- 4; 1), then x .
Sometimes equations with fractional terms are reduced to square ones. Consider the following equation.
Example 2. - =
Solution: When a = 0, it does not make sense, the value of x must satisfy the conditions: x -1, x -2. Multiplying all terms of the equation by a (x + 1) (x + 2) 0,
We get x 2 - 2 (a - 1) x + a 2 – 2a – 3 = 0, equivalent to the given one. Its roots:
x 1 \u003d a + 1, x 2 = - 3. Let's single out extraneous roots from these, i.e. those that are equal - 1 and - 2:
X 1 \u003d a + 1 \u003d - 1, a \u003d - 2, but with a \u003d - 2 x 2 = - 5;
X 1 \u003d a + 1 \u003d - 2, a \u003d - 3, but with a \u003d - 3 x 2 = - 6;
X 2 \u003d a - 3 \u003d - 1, a \u003d 2, but with a \u003d 2 x 1 = 3;
X 2 \u003d a - 3 \u003d - 2, a \u003d 1, but with a \u003d 1 x 1 = 2.
Answer: when a ≠ 0, a ≠ 2, a ≠ - 3, a ≠ 1 x 1 = a + 1, x 2 = a - 3;
When a \u003d - 2 x \u003d - 5; with a \u003d - 3 x \u003d - 6.
4.Method of solving quadratic equations under initial conditions.
The conditions of parametric quadratic equations are varied. For example, you need to find the value of the parameter at which the roots are: positive, negative, have different signs, more or less than some number, etc. To solve them, one should use the properties of the roots of the quadratic equation ax 2 + in + c = 0.
If D > 0, a > 0, then the equation has two real different roots, the signs of which for c > 0 are the same and opposite to the sign of the coefficient in, and for c
If D \u003d 0, a\u003e 0, then the equation has real and equal roots, the sign of which is opposite to the sign of the coefficient c.
If D 0, then the equation has no real roots.
Similarly, one can establish the properties of the roots of the quadratic equation for a
- If we interchange the coefficients a and c in a quadratic equation, we get an equation whose roots are inverse to the roots of the given one.
- If we change the sign of the coefficient in a quadratic equation, then we get an equation whose roots are opposite to the roots of the given one.
- If in a quadratic equation the coefficients a and c have different signs, then it has real roots.
- If a > 0 and D = 0, then the left side of the quadratic equation is a perfect square, and vice versa, if the left side of the equation is a perfect square, then a > 0 and D = 0.
- If all the coefficients of an equation are rational and the discriminant is a perfect square, then the roots of the equation are rational.
- If we consider the location of the roots relative to zero, then we apply the Vieta theorem.
Selection of the roots of a square trinomial according to the conditions and the location of the zeros of the quadratic function on the real line.
Let f (x) = ax 2 + in + c, a 0, roots x 1 ˂ x 2, ˂ .
Location of roots on a number line. | Necessary and sufficient condition. |
|
x 1, x 2 | a f () > 0, D 0, x 0 |
|
x 1, x 2 > | and f () > 0, D 0, x 0 > |
|
x 1 2 | a f ( ) |
|
1 x 2 . | and f ( ) > 0, D 0, and f ( ) > 0 0 . |
|
1 2 | and f ( ) > 0, and f ( ) |
|
x 1 2 | a f ( ) ) > 0 |
|
x 1 2 | a f ( ) ) |
Example 3 Determine for what values of a the equation
x 2 - 2 (a - 1) x + 2a + 1 = 0
- has no roots
necessary and sufficient condition D
D \u003d (a - 1) 2 - 2a - 1 \u003d a 2 - 4a
- has roots:
D 0, D \u003d (a - 1) 2 - 2a - 1 0, a
- has one root:
- has two roots:
D > 0, i.e. a
- has positive roots:
2(a – 1) > 0 a 4
If the question is “has two positive roots”, then the system should replace D > 0;
- has negative roots:
2(a - 1)
- has roots of different signs, i.e. one is positive and the other is negative:
a ;
Condition it is not necessary to use, it is enough x 1 x 2
- has one of the roots equal to 0:
a necessary sufficient condition is the equality to zero of the free term of the equation, i.e. 2a + 1 = 0, a = -1/2.
The sign of the second root is determined either by substitution into the original equation a = -1/2, or, more simply, by the Vieta theorem x 1 + x 2 \u003d 2 (a - 1), and after substituting a \u003d -1/2, we get x 2 = - 3, i.e. with a \u003d -1/2 two roots: x 1 \u003d 0, x 2 \u003d - 3.
Example 4 . At what values of the parameter a the equation
(a - 2) x 2 – 4ax +3 -2a = 0 has a unique solution that satisfies the inequality x
Solution.
Discriminant 2 - (a - 2) (3 - 2a)
4a 2 - 3a + 6 + 2a 2 - 4a = 6a 2 - 7a + 6
Since 49 - 144 \u003d - 95 and the first factor is 6 then 6а 2 – 7а + 6 for all x R.
Then x 1,2 = .
According to the condition of the problem x2, then we get the inequality
We have:
true for all a R.
6а 2 – 7а + 6 6а 2 – 7а - 10 2
And 1,2 \u003d 1/12 (7 17), and 1 \u003d 2, and 2 \u003d - 5/6.
Therefore, -5/6
Answer: -
5. Parameter as an equal variable.
In all the tasksthe parameter was treated as a fixed but unknown number. Meanwhile, from a formal point of view, a parameter is a variable, moreover, “equal” with others present in the example. For example, with this view of the form parameter f (x; a), functions are defined not with one (as before), but with two variables. Such an interpretation naturally forms another type (more precisely, a solution method that determines this type) of problems with parameters. Let us show an analytical solution of this type.
Example 5 On the xy plane, indicate all points through which none of the curves of the family y \u003d x passes through 2 - 4px + 2p 2 – 3, where p is a parameter.
Solution: If (x 0; y 0 ) is a point through which none of the curves of the given family passes, then the coordinates of this point do not satisfy the original equation. Consequently, the problem was reduced to finding the relationship between x and y, under which the equation given in the condition would have no solutions. The desired dependence is easy to obtain by focusing not on the variables x and y, but on the parameter p. In this case, a productive idea arises: consider the given equation as quadratic in p. We have
2p 2 - 4px + x 2 – y – 3 = 0. Discriminant= 8x 2 + 8y + 24 must be negative. From here we get y ˂ - x 2 - 3, therefore, the desired set is all points of the coordinate plane lying "under" the parabola y \u003d - x 2 – 3.
Answer: at 2 – 3
6. Technique for solving quadratic inequalities with parameters
In general.
Square (strict and non-strict) inequalities are called
Permissible are those values of the parameters for which a, b, c are valid. It is convenient to solve quadratic inequalities either analytically or graphically. Since the graph of a quadratic function is a parabola, then for a > 0 the branches of the parabola are directed upwards, for a
Different positions of the parabola f (x) = ax 2 + in + s, a 0 for a > 0 is shown in Fig.1
A) c) c)
a) If f (x) > 0 and D R;
b) If f (x) > 0 and D = 0, then x ;
c) If f (x) > 0 and D > 0, then x (- ; x 1 ) (x 2 ; + ).
The positions of the parabola are considered similarly for a
For example, one of the three cases where
when a 0 and f (x) > 0 x (x 1; x 2);
at a 0 and f (x) (- ; x 1 ) (x 2 ; + ).
As an example, consider the solution of an inequality.
Example 6 Solve inequality x 2 + 2x + a > 0.
Let D be the discriminant of the trinomial x 2 + 2x + a > 0. For D = 0, for a = 1, the inequality takes the form:
(x + 1) 2 > 0
It is true for any actual values x, except x = - 1.
For D > 0, i.e. at x, trinomial x 2 + 2x + a has two roots: - 1 - And
1 + and the solution of the inequality is the interval
(- ; - 1 – ) (- 1 + ; + )
This inequality is easy to solve graphically. To do this, we represent it in the form
X 2 + 2x > - a
and plot the function y = x 2 + 2x
The abscissas of the points of intersection of this graph with the straight line y \u003d - a and are the roots of the equation x 2 + 2x = - a.
Answer:
when –a > - 1, i.e. at a, x (- ; x 1 ) (x 2 ;+ );
at – a = - 1, i.e. with a = 1, x is any real number, except for - 1;
at - a , i.e. for a > 1, x is any real number.
Example 7 . Solve the inequality cx 2 - 2 (s - 1) x + (s + 2)
When c \u003d 0, it takes the form: 2x + 2the solution is x
We introduce the notation f (x) = cx 2 - 2 (s - 1) x + (s + 2) where c ≠ 0.
In this case, the inequality f (x)
Let D be the discriminant of f(x). 0.25 D = 1 - 4s.
If D > 0, i.e. if with> 0.25, then the sign of f (x) coincides with the sign of c for any real values of x, i.e. f(x)> 0 for any x R, hence, for c > 0.25 inequality f (x)
If D = 0, i.e. c \u003d 0.25, then f (x) \u003d (0.25 x + 1.5) 2 , i.e. f (x) 0 for any
X R. Therefore, for c = 0.25, the inequality f (x)
Consider the case D 0). f (x) = 0 for two real values of x:
x 1 \u003d (s - 1 -) and x 2 \u003d (s - 1 +).
There may be two cases here:
Solve the inequality f(x)
f (x) coincides with the sign of c. To answer this question, note that − , i.e. s – 1 – ˂ s – 1 + , but since with (with - 1 - ) (s – 1 + ) and therefore the solution of the inequality will be:
(- ; (s - 1 - )) ( (s - 1 + ); + ).
Now, to solve the inequality, it suffices to indicate those values of c for which the sign of f (x) is opposite to the sign of c. Since at 0 1 2, then x (x 1; x 2).
Answer: at c = 0 x R;
With (- ; x 2 ) (x 1 ; + );
At 0 (x 1; x 2);
For с 0.25 there are no solutions.
The view of the parameter as an equal variable is reflected in the graphical methods of solving and quadratic inequalities. Indeed, since the parameter is “equal in rights” with the variable, it is natural for it to “allocate” its own coordinate axis. Thus, a coordinate plane (x; a) arises. Such a minor detail as the rejection of the traditional choice of the letters x and y to designate axes defines one of the most best practices solving problems with parameters.
It is convenient when the problem contains one parameter a and one variable x. The solution process itself looks like this. First, a graphical image is built, then, crossing the resulting graph with straight lines perpendicular to the parametric axis, we “remove” the necessary information.
The rejection of the traditional choice of the letters x and y to designate the axes determines one of the most effective methods for solving problems with parameters - the "domain method"
- Method for solving quadratic inequalities under initial conditions.
Let us consider an analytical solution of a quadratic inequality with parameters, the results of which are considered on the real line.
Example 8
Find all x values for each of which the inequality
(2-x)a 2 + (x 2 -2x + 3)a-3x≥0
is performed for any value a belonging to the interval [-3; 0].
Solution. We transform the left side of this inequality as follows:
(2-x) a 2 + (x 2 -2x + 3) a-3x \u003d ax 2 - a 2 x - 2ax + 2a 2 + 3a - 3x \u003d
Ax (x - a) -2a (x - a) - 3 (x-a) \u003d (x - a) (ax - 2a - 3).
This inequality will take the form: (x - a) (ax - 2a - 3) ≥ 0.
If a = 0, we get - Зх ≥ 0 x ≤ 0.
If a ≠ 0, then -3 a
Because A 0, then the solution to this inequality will be the interval of the numerical axis, located between the roots of the equation corresponding to the inequality.
Let's find out the mutual arrangement of numbers a and , taking into account the condition - 3 ≤ a
3 ≤a
A = -1.
In all considered cases, we present the solutions of this inequality depending on the values of the parameter:
We get that only x = -1 is the solution to this inequality for any value of the parameter a .
Answer: -1
- Conclusion.
Why was I chosen a project on the topic “Development of methodological recommendations for solving quadratic equations and inequalities with parameters”? Since when solving any trigonometric, exponential, logarithmic equations, inequalities, systems, we most often come to consider sometimes linear, and most often quadratic equations and inequalities. When solving the most complex problems with parameters, most tasks are reduced with the help of equivalent transformations to the choice of solutions of the type: a (x - a) (x - c) > 0 (
We have reviewed theoretical basis for solving quadratic equations and inequalities with parameters. We remembered the necessary formulas and transformations, considered various arrangements of graphs of a quadratic function depending on the value of the discriminant, on the sign at the highest coefficient, on the location of the roots, the vertex of the parabola. We identified a scheme for solving and selecting results, compiled a table.
The project shows analytical and graphical methods for solving quadratic equations and inequalities. Students in a vocational school need visual perception of the material for better assimilation of the material. It is shown how you can change the variable x and accept the parameter as an equal value.
For a visual assimilation of this topic, the solution of 8 tasks with parameters, 1 - 2 for each section, is considered. Example 1 considers the number of solutions for different values parameter, in example No. 3, the solution of the quadratic equation is analyzed under a variety of initial conditions. A graphic illustration is made to solve quadratic inequalities. In example No. 5, the method of replacing the parameter as an equal value is used. The project includes consideration of example No. 8 from the tasks included in section C, for intensive preparation for passing the exam.
For high-quality training of students in solving problems with parameters, it is recommended to use multimedia technologies in full, namely: use presentations for lectures, electronic textbooks and books, own developments from the media library. Binary lessons of mathematics + computer science are very effective. The Internet is an irreplaceable assistant to the teacher and the student. Presentation requires imported objects from existing educational resources. The most convenient and acceptable in work is the DER "Using Microsoft Office at school".
The development of methodological recommendations on this topic will facilitate the work of young teachers who came to work at the school, replenish the teacher's portfolio, serve as a model for special subjects, sample solutions will help students cope with complex tasks.
- Literature.
1. Gorshtein P.I., Polonsky V.B., Yakir M.S. Tasks with parameters. "Ileksa", "Gymnasium", Moscow - Kharkov, 2002.
2. Balayan E.N. Collection of tasks in mathematics to prepare for the exam and olympiads. 9-11 grades. "Phoenix", Rostov-on-Don, 2010.
3. Yastrebinetsky G.A. Tasks with parameters. M., "Enlightenment", 1986.
4. Kolesnikova S.I. Mathematics. Solution challenging tasks Unified State Exam. M. "IRIS - press", 2005.
5. Rodionov E.M., Sinyakova S.L. Mathematics. Allowance for entering universities. The educational center"Landmark" MSTU im. N.E. Bauman, M., 2004.
6. Scanavi M.I. Collection of tasks in mathematics for applicants to universities: In 2 books. Book 1, M., 2009.
Solving inequalities with a parameter.
Inequalities that have the form ax > b, ax< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются linear inequalities.
The principles for solving linear inequalities with a parameter are very similar to the principles for solving linear equations with a parameter.
Example 1
Solve the inequality 5x - a > ax + 3.
Solution.
First, let's transform the original inequality:
5x - ax > a + 3, we take out the brackets x on the left side of the inequality:
(5 - a) x > a + 3. Now consider the possible cases for the parameter a:
If a > 5 then x< (а + 3) / (5 – а).
If a = 5, then there are no solutions.
If a< 5, то x >(a + 3) / (5 - a).
This solution will be the answer to the inequality.
Example 2
Solve the inequality x(a - 2) / (a - 1) - 2a / 3 ≤ 2x - a for a ≠ 1.
Solution.
Let's transform the original inequality:
x(a - 2) / (a - 1) - 2x ≤ 2a/3 - a;
Ah/(a – 1) ≤ -a/3. Multiply by (-1) both parts of the inequality, we get:
ax/(a – 1) ≥ a/3. Let's explore the possible cases for the parameter a:
1 case. Let a/(a – 1) > 0 or a € (-∞; 0)ᴗ(1; +∞). Then x ≥ (а – 1)/3.
2nd case. Let a/(а – 1) = 0, i.e. a = 0. Then x is any real number.
3rd case. Let a/(а – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.
Answer: x € [(a - 1) / 3; +∞) for a € (-∞; 0)ᴗ(1; +∞);
x € [-∞; (a – 1)/3] for a € (0; 1);
x € R for a = 0.
Example 3
Solve the inequality |1 + x| ≤ ax with respect to x.
Solution.
It follows from the condition that the right side of the inequality ax must be non-negative, i.e. ax ≥ 0. By the modulo expansion rule, the inequality |1 + x| ≤ ax we have a double inequality
Ax ≤ 1 + x ≤ ax. We rewrite the result in the form of a system:
(ax ≥ 1 + x;
(-ax ≤ 1 + x.
Let's transform to the form:
((а – 1)x ≥ 1;
((a + 1)x ≥ -1.
We investigate the resulting system on intervals and at points (Fig. 1):
For a ≤ -1 x € (-∞; 1/(a - 1)].
At -1< а < 0 x € [-1/(а – 1); 1/(а – 1)].
When a \u003d 0 x \u003d -1.
At 0< а ≤ 1 решений нет.
Graphical method for solving inequalities
Plotting greatly simplifies the solution of equations containing a parameter. The use of the graphical method in solving inequalities with a parameter is even clearer and more expedient.
Graphical solution of inequalities of the form f(x) ≥ g(x) means finding the values of the variable x for which the graph of the function f(x) lies above the graph of the function g(x). To do this, it is always necessary to find the intersection points of the graphs (if they exist).
Example 1
Solve the inequality |x + 5|< bx.
Solution.
We build graphs of functions y = |x + 5| and y = bx (Fig. 2). The solution of the inequality will be those values of the variable x for which the graph of the function y = |x + 5| will be below the graph of the function y = bx.
The figure shows:
1) For b > 1, the lines intersect. The abscissa of the intersection point of the graphs of these functions is the solution of the equation x + 5 = bx, whence x = 5/(b - 1). The graph y \u003d bx is higher for x from the interval (5 / (b - 1); +∞), which means that this set is the solution to the inequality.
2) Similarly, we find that at -1< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).
3) For b ≤ -1 x € (-∞; 5/(b - 1)).
4) For 0 ≤ b ≤ 1, the graphs do not intersect, which means that the inequality has no solutions.
Answer: x € (-∞; 5/(b - 1)) for b ≤ -1;
x € (-5/(b + 1); 5/(b – 1)) at -1< b < 0;
there are no solutions for 0 ≤ b ≤ 1; x € (5/(b – 1); +∞) for b > 1.
Example 2
Solve the inequality a(a + 1)x > (a + 1)(a + 4).
Solution.
1) Let's find the "control" values for the parameter a: a 1 = 0, a 2 = -1.
2) Let's solve this inequality on each subset of real numbers: (-∞; -1); (-1); (-10); (0); (0; +∞).
a) a< -1, из данного неравенства следует, что х >(a + 4)/a;
b) a \u003d -1, then this inequality will take the form 0 x > 0 - there are no solutions;
c)-1< a < 0, из данного неравенства следует, что х < (a + 4)/a;
d) a = 0, then this inequality has the form 0 x > 4 – there are no solutions;
e) a > 0, this inequality implies that x > (a + 4)/a.
Example 3
Solve the inequality |2 – |x||< a – x.
Solution.
We plot the function y = |2 – |x|| (Fig. 3) and consider all possible cases of the location of the line y \u003d -x + a.
Answer: the inequality has no solutions for a ≤ -2;
x € (-∞; (a - 2)/2) with a € (-2; 2];
x € (-∞; (a + 2)/2) for a > 2.
When solving various problems, equations and inequalities with parameters, a significant number of heuristic techniques open up, which can then be successfully applied in any other branches of mathematics.
Problems with parameters play an important role in the formation of logical thinking and mathematical culture. That is why, having mastered the methods of solving problems with parameters, you will successfully cope with other problems.
Do you have any questions? Don't know how to solve inequalities?
To get help from a tutor -.
The first lesson is free!
blog.site, with full or partial copying of the material, a link to the source is required.
State budgetary educational institution
Samara region secondary general education
school number 2 im. V. Maskina railway Art. Klyavlino
municipal district Klyavlinsky
Samara region
« Equations
And
inequalities
with parameters"
tutorial
Klyavlino
"Equations and inequalities with parameters" for students in grades 10-11
this manual is an appendix to the program of the elective course "Equations and inequalities with parameters", which has passed an external examination (scientific and methodological expert council of the Ministry of Education and Science of the Samara Region dated December 19, 2008, the ball is recommended for use in educational institutions Samara region)
Authors
Romadanova Irina Vladimirovna
Mathematics teacher, Klyavlinskaya Secondary General Education
school number 2 them. V. Maskina, Klyavlinsky district, Samara region
Serbaeva Irina Alekseevna
Introduction……………………………………………………………3-4
Linear equations and inequalities with parameters……………..4-7
Quadratic equations and inequalities with parameters……………7-9
Fractional rational equations with parameters……………..10-11
Irrational equations and inequalities with parameters……11-13
Trigonometric equations and inequalities with parameters.14-15
exponential equations and inequalities with parameters………16-17
Logarithmic equations and inequalities with parameters ...... 16-18
Tasks of the Unified State Examination………………………………………………………...18-20
Tasks for independent work…………………………...21-28
Introduction.
Equations and inequalities with parameters.
If in an equation or inequality some coefficients are not given by specific numerical values, but are indicated by letters, then they are called parameters, and the equation or inequality itself parametric.
In order to solve an equation or inequality with parameters, you must:
Highlight special meaning- this is the value of the parameter in which or when passing through which the solution of the equation or inequality changes.
Define allowed values are the parameter values at which the equation or inequality makes sense.
Solving an equation or inequality with parameters means:
1) determine at what values of the parameters solutions exist;
2) for each admissible system of parameter values, find the corresponding set of solutions.
An equation with a parameter can be solved by the following methods: analytical or graphical.
Analytical Method assumes the task of investigating the equation by considering several cases, none of which can be missed.
The solution of the equation and inequality with the parameters of each type by the analytical method involves detailed analysis situations and consistent research, during which the need arises "gentle handling" with a parameter.
Graphic method involves the construction of a graph of the equation, by which it is possible to determine how, respectively, the change in the parameter affects the solution of the equation. The graph sometimes allows one to analytically formulate the necessary and sufficient conditions for solving the set tasks. The graphical solution method is especially effective when it is necessary to establish how many roots the equation has depending on the parameter and has the undoubted advantage of seeing this visually.
§ 1. Linear equations and inequalities.
Linear Equation A x = b , written in general form, can be considered as an equation with parameters, where x – unknown , a , b - options. For this equation, the special or control value of the parameter is the one at which the coefficient vanishes in the unknown.
When solving a linear equation with a parameter, cases are considered when the parameter is equal to its special value and different from it.
Special parameter value a is the value A = 0.
b = 0 is a special parameter value b .
At b ¹ 0 the equation has no solutions.
At b = 0 the equation will take the form: 0x = 0. The solution to this equation is any real number.
Inequalities of the form ah > b And ax < b (a ≠ 0) are called linear inequalities. The set of solutions to the inequality ah >b– interval
(; +
),
If a
> 0
, And (-;)
, If A< 0
. Similarly for the inequality
Oh<
b
set of solutions - interval(-;),
If a
> 0,
And (; +),
If A< 0.
Example 1 solve the equation ax = 5
Solution: This linear equation.
If a = 0, then the equation 0 × x = 5 has no solution.
If A¹ 0, x =- solution of the equation.
Answer: at A¹ 0, x=
for a = 0 there is no solution.
Example 2 solve the equation ax - 6 \u003d 2a - 3x.
Solution: This is a linear equation ax - 6 \u003d 2a - 3x (1)
ax + 3x = 2a +6
Rewriting the equation as (a+3)x = 2(a+3) Let's consider two cases:
a= -3 And A¹ -3.
If a= -3, then any real number X is the root of equation (1). If A¹ -3 , equation (1) has a single root x = 2.
Answer: At a = -3, x 
R
;
at A
¹
-3, x = 2.
Example 3 At what values of the parameter A among the roots of the equation
2x - 4x - a 2 + 4а – 4 = 0 there are more roots 1 ?
Solution: Solve the equation 2x - 4x - a 2 + 4а – 4 = 0– linear equation
2 (a - 2) x \u003d a 2 - 4a +4
2(a - 2) x \u003d (a - 2) 2
At a = 2 solution of the equation 0x = 0 be any number, even greater than 1.
At A¹
2 x = 
.
By condition x > 1, that is >1, a > 4.
Answer: At A (2) U(4;∞).
Example 4 . For each parameter value A find the number of roots of the equation ax=8.
Solution. ax = 8 is a linear equation.
y = a– a family of horizontal lines;
y = - the graph is a hyperbola. We construct graphs of these functions.
Answer: If a = 0, then the equation has no solutions. If a ≠ 0, then the equation has one solution.
Example 5 . Using graphs, find out how many roots the equation has:
|x| = ax - 1.
y=| x | ,
y = ax - 1- the graph is a straight line passing through a point (0;-1).
We construct graphs of these functions.
Answer: When |a|>1- one root
at | a|≤1 The equation has no roots.
Example 6 . Solve the inequality ax + 4 > 2x + a 2
Solution
:
ax + 4 > 2x + a
2
(а – 2) х >A
2
– 4. Consider three cases.
Answer. x > a + 2 at a > 2; X<а + 2, at A< 2; at a=2 there are no solutions.
§ 2. Quadratic equations and inequalities
Quadratic equation is an equation of the form Oh ² + b x + c = 0 , Where a≠ 0,
A, b , With - options.
To solve quadratic equations with a parameter, you can use the standard methods of solving using the following formulas:
1
)
discriminant of the quadratic equation:
D
=
b
² - 4
ac
,
(
²-
ac)
2)
formulas of the roots of the quadratic equation:X
1
=
, X
2
=
,
(X
1,2 =
)
Square inequalities are called inequalities of the form
a X 2 + b x + c > 0,a X 2 + b x + c< 0, (1), (2)
a X 2 + b x + c ≥ 0,a X 2 + b x + c ≤ 0,(3), (4)
The set of solutions to inequality (3) is obtained by combining the sets of solutions to inequality (1) and the equation , a X 2 + b x + c=0. The set of solutions to inequality (4) is found similarly.
If the discriminant of a square trinomial
a
X
2
+
b
x + c
less than zero, then for a > 0 the trinomial is positive for all x R.
If the square trinomial has roots (x 1
< х
2
), then for a > 0 it is positive on the set(-;
x 2 )
(X 2;
+)
and negative on the interval
(x 1; x 2 ). If a< 0, то трехчлен положителен на интервале (х
1 ; x 2 ) and is negative for all x (-;
x 1 )(X 2;
+).
Example 1 solve the equation ax² - 2 (a - 1) x - 4 \u003d 0.
This is a quadratic equation
Solution: Special meaning a = 0.
At a = 0 we get a linear equation 2x - 4 = 0. It has a single root x = 2.
At a ≠ 0. Let's find the discriminant.
D \u003d (a-1)² + 4a \u003d (a + 1)²
If a = -1, That D = 0 - one root.
Find the root by substituting a = -1.
-x² + 4x - 4 \u003d 0, that is x² -4x + 4 = 0, we find that x=2.
If a ≠ - 1, That D
>0
. According to the root formula, we get:x= 
;
X 1 =2, x 2 = -.
Answer: At a=0 and a=-1 equation has one root x = 2; at a ≠ 0 and
A ≠ - 1 equation has two rootsX 1 =2, x 2 =-.
Example 2 Find the number of roots of the given equation x²-2x-8-a=0 depending on parameter values A.
Solution. Let us rewrite this equation in the form x²-2x-8=a
y \u003d x²-2x-8- the graph is a parabola;
y =a- a family of horizontal lines.
Let's build graphs of functions.
Answer: When A<-9 , the equation has no solutions; when a=-9, the equation has one solution; at a>-9, the equation has two solutions.
Example 3 At what A inequality (a - 3) x 2 – 2ax + 3a – 6 >0 holds for all values of x?
Solution. The square trinomial is positive for all values of x if
a-3 > 0 and D<0, т.е. при а, удовлетворяющих системе неравенств
,
whence it follows thata
> 6
.
Answer.a > 6
§ 3. Fractional-rational equations with a parameter,
reduced to linear
The process of solving fractional equations is carried out according to the usual scheme: the fractional is replaced by an integer by multiplying both parts of the equation by the common denominator of its left and right parts. After that, the whole equation is solved, excluding extraneous roots, that is, numbers that turn the denominator to zero.
In the case of equations with a parameter, this problem is more complicated. Here, in order to “eliminate” extraneous roots, it is required to find the value of the parameter that turns the common denominator to zero, that is, to solve the corresponding equations for the parameter.
Example 1
solve the equation 
= 0
Solution: D.Z: x +2 ≠ 0, x ≠ -2
x - a \u003d 0, x \u003d a.
Answer: At a ≠ - 2, x=a
At a = -2 there are no roots.
Example 2
.
solve the equation 
- 
= 
(1)
This is a fractional rational equation
Solution: Meaning a = 0 is special. At a = 0 the equation loses its meaning and, therefore, has no roots. If a ≠ 0, then after transformations the equation will take the form: x² + 2 (1-a) x + a² - 2a - 3 = 0 (2)- quadratic equation.
Let's find the discriminant 
\u003d (1 - a)² - (a² - 2a - 3) \u003d 4,
find the roots of the equationX
1
= a + 1, x
2
= a - 3.
When passing from equation (1) to equation (2), the domain of definition of equation (1) expanded, which could lead to the appearance of extraneous roots. Therefore, verification is necessary.
Examination. Exclude from found values X those in which
x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0.
If X 1 +1=0, that is (a+1) + 1= 0, That a = -2. Thus,
at a= -2 , X 1 -
If X 1 +2=0, that is (a+1)+2=0, That a = - 3. Thus, at a \u003d - 3, x 1 - extraneous root of the equation. (1).
If X 2 +1=0, that is (a - 3) + 1= 0, That a = 2. Thus, at a = 2 x 2 - extraneous root of equation (1).
If X 2 +2=0, that is ( a – 3) + 2 = 0, That a=1. Thus, at a = 1,
X 2 - extraneous root of equation (1).
In accordance with this, a = - 3 we get x \u003d - 3 - 3 \u003d -6;
at a \u003d - 2 x \u003d -2 – 3= - 5;
at a \u003d 1 x \u003d 1 + 1 \u003d 2;
at a \u003d 2 x \u003d 2 + 1 \u003d 3.
You can write down the answer.
Answer: 1) if a= -3, That x= -6; 2) if a= -2, That x= -5; 3) if a=0, then there are no roots; 4) if a=1, That x=2; 5) if a=2, That x=3; 6) if a ≠ -3, a ≠ -2, a ≠ 0, a ≠ 1, a ≠ 2, then x 1 = a + 1, x 2 = a-3.
§4. Irrational equations and inequalities
Equations and inequalities in which the variable is contained under the root sign are called irrational.
The solution of irrational equations is reduced to the transition from an irrational to a rational equation by raising both sides of the equation to a power or by changing the variable. When both sides of the equation are raised to an even power, extraneous roots may appear. Therefore, when using this method, all found roots should be checked by substituting into the original equation, taking into account changes in the parameter values.
Type equation 
=g (x ) is equivalent to the system 
The inequality f (x) ≥ 0 follows from the equation f (x) = g 2 (x).
When solving irrational inequalities, we will use the following equivalent transformations:
≤ g(x) 
≥g(x) 
Example 1
Solve the Equation 
= x + 1 (3)
This irrational equation
Solution:
By definition of the arithmetic root, equation (3) is equivalent to the system 
.
At a = 2 the first equation of the system has the form 0 x = 5, that is, it has no solutions.
At a≠ 2 x= 
.
Let us find out for what valuesA
found valueX
satisfies the inequalityx ≥ -1: ≥ - 1, 
≥ 0,
where a ≤ or a > 2.
Answer: At a≤, a > 2 x= ,
at < а ≤ 2
the equation has no solutions.
Example 2
solve the equation 
= a
(Annex 4)
Solution. y
=
y = a is a family of horizontal lines.
Let's build graphs of functions.
Answer: at A<0 - there are no solutions
at A≥ 0 - one solution.
Example 3
. Let's solve the inequality(a+1) 
<1.
Solution. O.D.Z. x ≤ 2. If a+1 ≤0, then the inequality holds for all admissible values X. If a+1>0, That
(a+1) <1.<
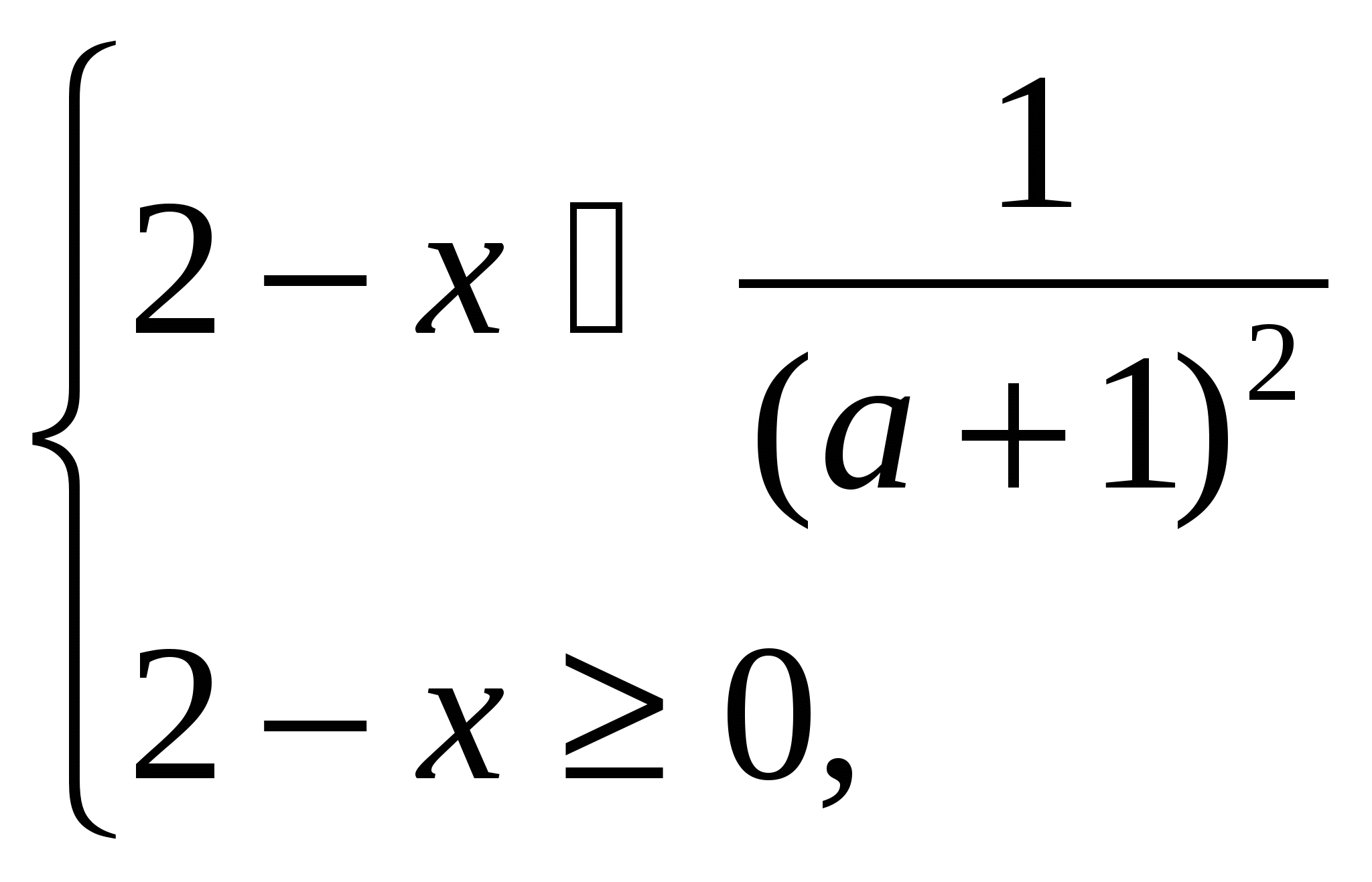
where X (2- 
2
Answer.
X (- ;2at a (-;-1,
X (2- 2
at A
(-1;+).
§ 5. Trigonometric equations and inequalities.
Here are the formulas for solving the simplest trigonometric equations:
Sinx = a x= (-1) n arcsin a+πn, n Z, 
≤1, (1)
Cos x = a x = ± arccos a + 2 πn, n Z, ≤1.
(2)
If
>1, then equations (1) and (2) have no solutions.
tan x = a x= arctg a + πn, n Z, a R
ctg x = a x = arcctg a + πn, n Z, a R
For each standard inequality, we indicate the set of solutions:
1.
sin x > a arcsin a + 2 n
Z,
at a
<-1,
x R
;
at a
≥ 1,
there are no solutions.
2. . sin x< a π - arcsin a + 2 πnZ,
for a≤-1, there are no solutions; when a>1,x R
3.
cos
x
>
a
-
arccos
a
+ 2
pn
<
x
<
arccos
a
+ 2
pn
,
n
Z
,
at A<-1,
x R
; at a
≥ 1
, there are no solutions.
4. cos x arccos a+ 2 nZ,
at a≤-1
, there are no solutions; ata
> 1,
x
R
5. tg x > a, arctg a + πnZ
6.tg x< a, -π/2 + πn Z
Example1. Find A, for which this equation has a solution:
Cos 2 x + 2(a-2) cosx + a 2 - 4a - 5 \u003d 0.
Solution. We write the equation in the form
Withos 2 x + (2 a -4) cosx +(a – 5)(а+1) =0, solving it as a square, we get cosx = 5-A And cosx = -a-1.
The equation cosx
= 5-
A
has solutions provided -1≤ 5-A
≤1
4≤
A≤ 6, and the equation cosx
= -
a-1
provided -1≤ -1-A
≤ 1
-2 ≤
A
≤0.
Answer.
A
-2; 0 4; 6
Example 2
At what bthere exists a such that the inequality 
+
b> 0 is satisfied for all x ≠pn
,
n
Z
.
Solution. Let's put A= 0. The inequality holds for b >0. Let us now show that no b ≤0 satisfies the conditions of the problem. Indeed, it suffices to put x = π /2, If A <0, и х = - π /2 at A ≥0.
Answer.b > 0
§ 6. Exponential equations and inequalities
1. Equation h(x)
f ( x )
=
h(x)
g ( x) at h(x) > 0 is equivalent to the combination of two systems 
And 
2. In a particular case (h (x)= a ) the equation A f(x) = A g(x) at A> 0, is equivalent to the combination of two systems
And 
3. Equation A f(x) = b , Where A > 0, a ≠1, b>0, is equivalent to the equation
f(x)= log a b . Happening A=1 are considered separately.
The solution of the simplest exponential inequalities is based on the degree property. Inequality of the formf(a
x ) > 0 by changing the variablet=
a
x reduces to solving the system of inequalities 
and then to the solution of the corresponding simplest exponential inequalities.
When solving a non-strict inequality, it is necessary to add the roots of the corresponding equation to the set of solutions of a strict inequality. As with solving equations in all examples containing the expression A f (x ) , we assume A> 0. Case A= 1 are considered separately.
Example 1
.
At what A equation 8 x = 
has only positive roots?
Solution.
By the property of an exponential function with a base greater than one, we have x>0 8
X >1 >1
>0, whencea
(1,5;4).
Answer.
a
(1,5;4).
Example 2 Solve the inequality a 2 ∙2 x > a
Solution. Consider three cases:
1.
A< 0
. Since the left side of the inequality is positive and the right side is negative, the inequality holds for any x R.
2. a=0. There are no solutions.
3.
A
> 0
.
a
2
∙2
x
> a
2
x
>
x > - log 2
a
Answer.
X R at A
> 0; no solutions for
a
=0; X (-
log 2
a; +) ata > 0
.
§ 7. Logarithmic equations and inequalities
Let us present some equivalences used in solving logarithmic equations and inequalities.
1. The equation log f (x) g (x) \u003d log f (x) h (x) is equivalent to the system
In particular, if A >0, A≠1, then
log a
g(x)=log a
h(x) 
2.
The equation log a
g(x)=b g(x)=a
b (
A
>0,
a ≠
1, g(x) >0).
3. Inequality log f ( x )
g (x) ≤
log f ( x )
h(x) is equivalent to the combination of two systems: 
And 
If a, b are numbers, a >0, a ≠1, then
log a
f(x) ≤ b 
log a
f(x) > b 
Example 1
Solve the Equation 
Solution. Let's find ODZ: x > 0, x ≠ A 4 , a > 0, A≠ 1. Transform the equation
log 
x - 2 = 4 - log a
x log x + log a
x– 6 = 0, whence log a
x = - 3
x = A-3 and log a
x = 2
x = A 2. Condition x = A
4
A
– 3
=
A 4 or A
2
=
A
4
not performed on the ODZ.
Answer: x = A-3, x = A 2 at A
(0; 1) 
(1; ).
Example 2 . Find the highest value A, for which the equation
2
log 
-
+
a
= 0 has solutions.
Solution.
Let's replace =
tand get the quadratic equation 2t 2
–
t +
a
= 0. Solving, we findD = 1-8
a
. Consider D≥0, 1-8
A
≥0 
A
≤.
At A = quadratic equation has a roott= >0.
Answer. A =
Example 3 . Solve the inequalitylog(x 2 – 2 x + a ) > - 3
Solution.
Let's solve the system of inequalities 
Roots of square trinomials x 1,2
= 1 ± 
their 3,4
= 1 ± 
.
Critical parameter values: A= 1 and A= 9.
Let X 1 and X 2 be the solution sets of the first and second inequalities, then
X 1 
X 2
= X is the solution to the original inequality.
At 0<
a
<1 Х
1
= (-
;1 - )(1 + ; +), atA> 1 x 1 = (-;+).
At 0<
a
< 9 Х
2
= (1 -; 1 +), atA≥9 Х 2 – no solutions.
Consider three cases:
1. 0<
a
≤1 X = (1 - ;1 - )(1 + ;1 +).
2. 1 <
a
< 9 Х = (1 -;1 +).
3. a≥ 9 Х – no solutions.
USE tasks
High level C1, C2
Example 1 Find all values R, for which the equation
R ∙ ctg 2x+2sinx+ p= 3 has at least one root.
Solution. Let's transform the equation
R ∙ (
-1)+2sinx+ p\u003d 3, sinx \u003d t, t 
, t 
0.
-
p+ 2t + p
= 3,
+ 2t = 3, 3 -2t = , 3t2 – 2t3 = p
.
Let f(y) = 3
t 2
– 2
t 3
. Let's find the set of function valuesf(x) on 
. at /
= 6
t – 6
t 2
, 6
t - 6
t 2
= 0,
t 1
=0,
t 2
= 1.
f(-1) = 5,
f(1) = 1.
At t ,
E(f) =
,
At t ,
E(f) =
, that is, when t ,
E(f) =
.
To Equation 3t 2
– 2
t 3
=
p
(hence the given) had at least one root necessary and sufficientp
E(f), that is p
.
Answer.
.
Example 2
At what values of the parameterA the equation log 
(4
x 2
– 4
a
+
a
2
+7) = 2 has exactly one root?
Solution. Let's transform the equation into an equivalent one:
4x 2 - 4 a + a 2 +7 \u003d (x 2 + 2) 2.
Note that if a certain number x is the root of the resulting equation, then the number - x is also the root of this equation. By condition, this is not feasible, so the only root is the number 0.
Let's find A.
4∙ 0 2 - 4a + a 2 +7 = (0 2 + 2) 2 ,
a 2 - 4a +7 = 4, a 2 - 4a +3 = 0, a 1 = 1, a 2 = 3.
Examination.
1)
a
1
= 1. Then the equation has the form:log (4
x 2
+4) =2. We solve it
4x 2 + 4 \u003d (x 2 + 2) 2, 4x 2 + 4 \u003d x 4 + 4x 2 + 4, x 4 \u003d 0, x \u003d 0 is the only root.
2)
a
2
= 3. The equation looks like:log (4
x 2
+4) =2 x = 0 is the only root.
Answer. 1; 3
High level C4, C5
Example 3 Find all values R, under which the equation
x 2 - ( R+ 3)x + 1= 0 has integer roots and these roots are solutions to the inequality: x 3 - 7 R x 2 + 2x 2 - 14 R x - 3x +21 R ≤ 0.
Solution.
Let x 1,
X 2
are the integer roots of the equation x 2
– (R
+ 3)x + 1= 0. Then, by the Vieta formula, x 1
+ x 2
=
R
+ 3, x 1
∙ x 2
= 1. The product of two integers x 1
, X 2
can be equal to one only in two cases: x 1
= x 2
= 1 or x 1
= x 2
= - 1. If x 1
= x 2
= 1, thenR
+ 3 = 1+1 = 2R
= - 1; if x 1
= x 2
= - 1, thenR
+ 3 = - 1 – 1 = - 2 R
= - 5. Check whether the roots of the equation x 2
– (R
+ 3)x + 1= 0 in the cases described by the solutions of this inequality. For the caseR
= - 1, x 1
= x 2
= 1 we have
1 3 - 7 ∙ (- 1) ∙ 1 2 +2 ∙ 1 2 - 14 ∙ (- 1) ∙ 1 - 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 - true; for the case R\u003d - 5, x 1 \u003d x 2 \u003d - 1 we have (- 1) 3 - 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 - 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 is correct. So, the condition of the problem is satisfied only R= - 1 and R = - 5.
Answer.R 1 = - 1 and R 2 = - 5.
Example 4 Find everything positive values parameter A, for which the number 1 belongs to the domain of the function
at
= (A 
-
A 
).
